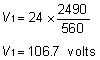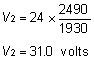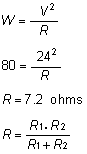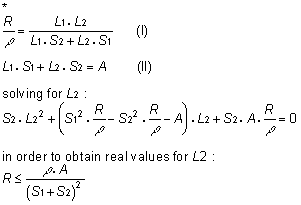|
Voltage Reduction
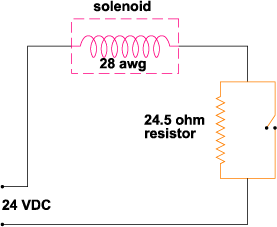
One method of consuming less energy is to apply a voltage to the solenoid coil to provide the necessary force to pull the plunger in, then, when seated, drop the voltage down to a level sufficient to maintain the plunger in a seated position. As an example, we may consider the following condition: Example: One particular design requires 20 ounces of force to move a linkage by 0.600 inches. Space allows for a 3/4 inch diameter by 1.50 inch long solenoid using a 24 volt DC supply. A good choice for this application would be the S-15-75 solenoid. Using the graph on the related page, it is observed that 24 ounces at 0.600 inches stroke can be obtained from a solenoid with approximately 2490 AT (slightly more force than actually needed). By referring to the coil data, 80 watts will be required to generate the 2490 ampere turns, but the solenoid cannot be left on for more than 8 seconds. The closest voltage in the related column in 23.6 volts DC which refers to a coil with 28 awg with an internal resistance of approximately 7 Ohms. Therefore, the proper solenoid is S-15-75-28. It should be noted that the 24 VDC supply will generate slightly more force than the required 23.6 VDC. When the plunger is seated, which means when the stroke is zero, the graphs indicate that only approximately 500 ampere turns will be required to generate approximately 24 ounces of force. If we consider 560 AT for hold, the voltage can be dropped to 5.3 volts. This results in 4 watts of power consumption. In this case the voltage can be left on indefinitely and power consumption will be dropped by approximately 95% in order to maintain the initial required force.
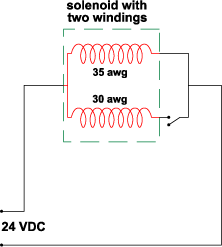
Another method of reducing the power consumption once the plunger is pulled in, is achieved by using a solenoid with multiple windings. In a case where two windings are used, initially when energized, both windings are electrically in parallel. When plunger is seated, one winding (usually the one that consumes more power) will be disconnected from the circuit, while allowing the other winding (with less power consumption) to remain energized, holding the plunger in position. In the previous example, in order to achieve the same amount of ampere turns by using a solenoid with two windings, the following format can be used: To obtain 560 ampere turns by using an 80 watt solenoid, the wire gauge can be selected by calculating the required voltage. The required ampere turns from hold winding is 560 AT.
The required ampere turns from the second winding is:
therefore:
According to the table the closest voltages to 106.7 volts and 31.0 volts are 92.2 volts and 29.7 volts, which refer to 34 awg and 29 awg respectively. ( We will find out in the following calculations that using both these gages at the same time is not possible and one or both must change. This is due to the fact that if we use these two windings, in order to achieve the necessary resistance values, a larger winding volume will be necessary.) In order to consume 80 watts of power at 24 volts, the parallel resistance must be 7.2 ohms.
Where R 1 and R2 are the resistance values of the first and second windings respectively.By replacing R 1 and R2 with
Where D is the resistivity of copper, L1 and L2 are the lengths and S1 and S2 are the cross sectional areas of wires used for the first and the second windings respectively.Denoting A as the useful volume of the bobbin for copper (60% of the total winding volume), we can write: S 1 C L1 + S2 C L2 = A (II)In equations (I) and (II), L 1 and L2 are the only unknowns. For L1 and L2 to have real values, the following condition must exist.*
Therefore, the necessary condition does not exist. This means that we must select a different gage wire for one or both windings. In the next step, we select 120 volts and 37.5 volts, which refer to 35 awg and 30 awg respectively. These voltages are both slightly higher than the actual required voltage, and as a result, as will be noticed later, the resulted ampere turns will be slightly lower than 560 AT and 1930 AT. By using the new values:
In this case;
which satisfies the requirement, therefore the new gages are valid. Solving equations (I) and (II): L1 = 2749 in., L2 = 920 in or, L1 = 540 in., L2 = 1613 in Assuming the average bobbin diameter to be 0.545 inches, and the resistivity of copper D = 6.79 x 10-7 ohm-in., and denoting N1 and N2 for the number of turns of wire for the first and second windings respectively:
As can be seen, two sets of values for L1 and L2 are obtained, and they are both valid. The values for A1T1, A2T2 and Wparallel = W1 + W2 are identical in both sets, which support the initial requirements. It is obvious that in our case the first set of answers will be used, due to smaller amount of steady state power consumption (W1 = 7.7 watts versus W1 = 39.2 watts), so the solenoid can be left on indefinitely.
In all the previous examples, to simplify the problem, mostly no safety factor was used and there were no considerations for losses of force due to the heat generation within the solenoid. It is very important to consider the heat related losses and a safety factor due to external frictions, since in many cases the differences could be substantial..
|